TS 35.234
Specification of the MILENAGE-256 algorithm set:
an example set of 256-bit 3GPP
Authentication and Key Generation
Functions f1, f1, f2, f3, f4, f5, f5 and f5**
Document 1: General

3GPP‑Page ETSI‑search

V19.0.0 (Wzip) 2024/12 18 p.

Rapporteur:: Mrs. Pauliac, Mireille
THALES

full Table of Contents for TS 35.234 Word version: 19.0.0

0 Introduction p. 5

The present document contains a 256-bit example of set of algorithms, collectively called MILENAGE-256, which may be used as the authentication and key generation functions f1, f1*, f2, f2, f3, f5, f5, f5* and f5**. It is not mandatory to use the particular algorithms specified in this document - all eight functions are operator-specifiable rather than being fully standardised. Operators electing to employ this example set can further personalise the algorithms (as described in the text). The present document is one of four documents, which collectively comprise the entire specification of the example authentication and key generation algorithms. Namely:

3GPP TS 35.234: "Specification of the MILENAGE-256 algorithm set: An example set of 256-bit 3GPP authentication and key generation functions f1, f1*, f2, f2, f3, f5, f5, f5* and f5**; Document 1: MILENAGE-256 General".
3GPP TS 35.235: "Specification of the MILENAGE-256 algorithm set: An example set of 256-bit 3GPP authentication and key generation functions f1, f1*, f2, f2, f3, f5, f5, f5* and f5**; Document 2: MILENAGE-256 Algorithm Specification".
3GPP TS 35.236: "Specification of the MILENAGE-256 algorithm set: An example set of 256-bit 3GPP authentication and key generation functions f1, f1*, f2, f2, f3, f5, f5, f5* and f5**; Document 3: Implementors' Test and Design Conformance Test Data".
3GPP TR 35.937: "Specification of the MILENAGE-256 algorithm set: An example set of 256-bit 3GPP authentication and key generation functions f1, f1*, f2, f2, f3, f5, f5, f5* and f5**; Document 4: Summary and Results of Design and Evaluation".

1 Scope p. 6

The present document contains a high level specification of the MILENAGE-256 algorithm set which constitutes an example set of 3GPP authentication and key generation functions with a 256-bit target security level.

The example set is based on the block cipher Rijndael-256-256 with 256-bit key and 256-bit block size [8], [14] (recall that the 128 bit Advanced Encryption Standard, AES-128, corresponds to Rijndael-128-128 [8]).

An optional-to-use function, f5**, was designed according to candidate solutions discussed in 3GPP SA3 (TR 33.846), with the aim of countering certain replay attacks that can lead to traceability of subscribers [13]. When used, the optional function f5** replaces f5*.

The specification and associated test data for the example algorithm set is documented in two documents:

A formal specification of the mode and the example kernel (TS 35.235).
A detailed test data document, covering mode and the example kernel (TS 35.236).

A detailed summary of the evaluation is provided in a public evaluation report (TR 35.937).

The present document provides an overview of the overall work.

2 References p. 6

The following documents contain provisions which, through reference in this text, constitute provisions of the present document.

References are either specific (identified by date of publication, edition number, version number, etc.) or non-specific.
For a specific reference, subsequent revisions do not apply.
For a non-specific reference, the latest version applies. In the case of a reference to a 3GPP document (including a GSM document), a non-specific reference implicitly refers to the latest version of that document in the same Release as the present document.

[1]

TR 21.905: "Vocabulary for 3GPP Specifications".

[2]

TS 35.235: "Specification of the MILENAGE-256 algorithm set: An example set of 256-bit 3GPP authentication and key generation functions f1, f1*, f2, f2, f3, f5, f5, f5* and f5**; Document 2: MILENAGE-256 Algorithm Specification".

[3]

TS 35.236: "Specification of the MILENAGE-256 algorithm set: An example set of 256-bit 3GPP authentication and key generation functions f1, f1*, f2, f2, f3, f5, f5, f5* and f5**; Document 3: Implementors' Test and Design Conformance Test Data".

[4]

TR 35.937: "Specification of the MILENAGE-256 algorithm set: An example set of 256-bit 3GPP authentication and key generation functions f1, f1*, f2, f2, f3, f5, f5, f5* and f5**; Document 4: Summary and Results of Design and Evaluation".

[5]

TS 33.102: "3rd Generation Partnership Project; Technical Specification Group Services and System Aspects; 3G Security; Security Architecture".

[6]

TS 33.105: "3rd Generation Partnership Project; Technical Specification Group Services and System Aspects; 3G Security; Cryptographic Algorithm Requirements".

[7]

TS 33.501: "Security architecture and procedures for 5G system".

[8]

Rijndael information page, NIST archived AES submissions, https://csrc.nist.gov/projects/cryptographic-standards-and-guidelines/archived- crypto-projects/aes-development#rijndael

[9]

The Advanced Encryption Standard (AES), NIST FIPS 197, 2001.

[10]

TS 35.205: "3rd Generation Partnership Project; Technical Specification Group Services and System Aspects; 3G Security; Specification of the MILENAGE Algorithm Set: An example algorithm set for the 3GPP authentication and key generation functions f1, f1*, f2, f3, f4, f5 and f5*; Document 1: General".

[11]

TS 35.231: "Specification of the TUAK algorithm set: A second example algorithm set for the 3GPP authentication and key generation functions f1, f1*, f2, f3, f4, f5 and f5*; Document 1: Algorithm specification".

[12]

TR 33.846: "Study on authentication enhancements in the 5G System (5GS)".

[13]

R. Borgaonkar, "New Privacy Threat on 3G, 4G, and Upcoming 5G AKA Protocols", in Proceedings on Privacy Enhancing Technologies 2019(3):108-127. Also available at https://eprint.iacr.org/2018/1175.pdf (published online: July 2019).

[14]

J. Daemen and V. Rijmen, "The design of Rijndael", Springer Verlag, 2002.

[15]

H. Gilbert: "The Security of One-Block-to-Many Modes of Operation", in T. Johansson (Ed): Proceedings of FSE 2003, LNCS 2887, Springer Verlag, pp. 376- 395.

[16]

A. Maximov and M. Näslund, "Security analysis of the Milenage-construction based on a PRF", Cryptology ePrint Archive, available at https://eprint.iacr.org/2023/607.

3 Definitions of terms, symbols, and abbreviations p. 7

3.1 Terms p. 7

For the purposes of the present document, the terms given in TR 21.905 and the following apply. A term defined in the present document takes precedence over the definition of the same term, if any, in TR 21.905.

AKA-specific terminology

AMF:

Authentication Management Field

AK:

Anonymity key

AK*:

Anonymity key used during resynchronisation

CK:

Cipher Key

f1, f1*, f2, f3, f4, f5, f5*, f5**:

Cryptographic functions used to derive AKA parameters

IK:

Integrity Key

Subscriber key

MAC-A:

Network Authentication Code

MAC-S:

Resynchronisation Authentication Code

RAND:

Random Challenge

RES:

Response to Challenge

SQN:

Sequence Number

SQN_HE:

Local value of SQN as available in the HE

SQN_MS:

Local value of SQN as available at the MS

XMAC-A:

Expected value of MAC-A

XMAC-S:

Expected value of MAC-S

XRES:

Expected Response to Challenge

Additional terminology

5G HE AV:

5G Home Environment AV, an AV consisting of RAND, AUTN, XRES*

ALGONAME:

An ASCII character string encoding of a name assigned for a particular instance/application of the MILENAGE-256 algorithm set instance

𝑐₀, 𝑐₁, 𝑐₂, 𝑐₃, 𝑐₄, 𝑐₅, 𝑐₆, 𝑐₇:

128-bit operator-customisable constants, used during the computation of f1, f1*, f2, f3, f4, f5, f5*, and f5**

𝐼𝑁₀, 𝐼𝑁₁, 𝐼𝑁₂, 𝐼𝑁₃, 𝐼𝑁₄, 𝐼𝑁₅, 𝐼𝑁₆, 𝐼𝑁₇:

256-bit instance-specific input values constructed within the computation of the functions f1, f1*, f2, f3, f4, f5, f5*, and f5**

K_SZ:

The length of the subscriber key K, in octets

K_AUSF:

5G-specific key, resulting from post-processing of CK and IK

OP:

A 256-bit Operator Variant Algorithm Configuration Field that is a component of the functions f1, f1*, f2, f3, f4, f5, f5* and f5**

𝑂𝑃_C:

A 256-bit value derived from OP, ALGONAME, KSZ and K, and used within the computations of the functions f1, f1*, f2, f3, f4, f5, f5* and f5**

RES*:

5G-specific, post-processed RES value

A 256-bit intermediate value constructed from ALGONAME and KSZ, and used in the computation of 𝑂𝑃_C

XRES*:

5G-specific, post-processed XRES value

3.2 Symbols p. 8

For the purposes of the present document, the following symbols apply:

The assignment operator

The definition operator

⊕

The bitwise exclusive-OR operation

∥

The concatenation of the two operands

E_K(X)

Encryption of X under key K

PRF_K

Pseudo-random function defined by key K

Rijndael-b-n

Rijndael block cipher with b-bit block and n-bit key

3.3 Abbreviations p. 8

For the purposes of the present document, the abbreviations given in TR 21.905 and the following apply. An abbreviation defined in the present document takes precedence over the definition of the same abbreviation, if any, in TR 21.905.

3GPP

3rd Generation Partnership Project

AES

Advanced Encryption Standard

AKA

Authentication and Key Agreement

ARPF

Authentication Repository Function

ASCII

American Standard Code for Information Interchange

AUTS

Re-synchronisation Token

Authentication Vector

DPA

Differential Power Analysis

Electromagnetic Emanations

eSIM

Embedded SIM

Home Environment

MAC

Message Authentication Code

MDPH

Merkle-Damgård with Permutation and Hirose compression function

Mobile Equipment

Mobile Station

PRF

Pseudo-Random Function

PRP

Pseudo-Random Permutation

SPA

Simple Power Analysis

Timing Attack

UDM

Unified Data Management

User Equipment

UICC

Universal Integrated Circuit Card

USIM

Universal Subscriber Identity Module

4 Structure p. 9

This specification is organised as follows:

Clause 5 provides background information on the Authentication and Key Generation algorithms.
Clause 6 provides background information on security and functional requirements on the algorithms and their use.
Clause 7 describes how the algorithms were designed and how the specification and associated test data were produced.
Clause 8 gives an overview of the evaluation work and the conclusions of the evaluations.

5 Background to the 3GPP Authentication and Key Agreement Algorithm p. 9

Within the mobile communication systems specified by 3GPP, there is a need to provide security features. These security features have gradually increased in sophistication and security level from the 3rd generation (UMTS) networks up to the current 5th (5G) generation (TS 33.105), and are realised with the use of cryptographic functions and algorithms. One such set of algorithms is the authentication and key generation algorithms. These algorithms, called f1, f1*, f2, f3, f4, f5, f5*, are not standardised, allowing each operator to freely construct proprietary algorithms. The context for these algorithms is described for 3G usage in TS 33.102 and remains valid in 5G. The generic requirements for these algorithms are specified in TS 33.105, which, apart from a desire to increase security level and flexibility (see below) also largely remain valid.

For 5G, an optional-to-use alternative to f5*, denoted f5** is also defined in order to thwart some recently discovered attacks on privacy. Further, in order for the algorithm to be both future proof and backward compatible, the new algorithm is set to accept inputs of varying size, as well as being able to produce outputs of variable size.

These algorithms can in principle be chosen by each operator without causing interoperability problems as long as the input/output parameters agree with the formats defined in the 3GPP specifications. However, to enable secure instantiation of the algorithm set, one or more concrete example algorithm sets is highly beneficial and to simultaneously meet operator customisation requirements, such algorithm sets should be configurable by parameters that create operator-specific instances, without risk of affecting security negatively.

Two such algorithm sets have been defined in the past: MILENAGE and TUAK (TS 35.205, TS 35.231). For future-proof usage (e.g. resistance to quantum computing), it becomes necessary to support keys larger than 128 bits. This support already exists for TUAK but not for MILENAGE. These two algorithm sets also differ in terms of using different kernels (a hash function and a block cipher, respectively) and retaining this diversity at the 256-bit security level was judged to be desirable. For this reason, an upgraded version of MILENAGE is defined with a 256-bit target security level, denoted MILENAGE-256.

With MILENAGE being based on AES [9], a natural choice for kernel of MILENAGE-256 is just to "scale up" by instead using the Rijndael block cipher with 256-bit key and block size ([8], [14]). This is because Rijndael-256-256 is structurally very similar to AES-256 and Rijndael-128-256 is exactly identical to AES-256. Kernel is however provably secure under certain assumptions on the underlying block-cipher, with quantitatively similar security bounds.

6 Outline of algorithm requirements specifications p. 10

The basic requirements for the authentication and key generation functions were specified in TS 33.105.

Additionally, a recently discovered subscriber-tracing attack [13] led to defining an optional-to-use function f5** according to candidate solutions discussed in TR 33.846.

6.1 The Authentication and Key Generation Functions p. 10

The mechanism for authentication and key agreement (TS 33.102) requires the following cryptographic functions:

the random challenge generating function;

the network authentication function;

f1*

the re-synchronisation message authentication function;

the user authentication function;

the cipher key derivation function;

the integrity key derivation function;

the anonymity key derivation function;

f5*

the anonymity key derivation function for the re-synchronisation message.

Additionally, the present document defines:

f5**

an alternative to f5* which provides additional protection against subscriber tracing.

An example for the random challenge generation function, f0, is not proposed.

For each of the algorithms f1 to f5* (and f5**), it is required that it should be computationally infeasible to derive the subscriber key K using knowledge of the input(s) and output (other than K itself). Further requirements assumed to hold for the current 128-bit MILENAGE algorithm set, e.g. that outputs are computationally unpredictable and indistinguishable from random bits, also need to be met by MILENAGE-256.

For the specific case when the f-functions are provided by MILENAGE-256, the structure follows the framework of Figure 7.2-1.

The following clauses describe the usage of the algorithms on the network side and the terminal side. Under normal operation, the process is initiated on the network side as described in clause 6.2, followed by corresponding processing in the terminal in clause 6.3. If a re-synchronisation procedure is required (as determined by clause 6.3), the processing of clause 6.4 next takes place, followed by the processing of clause 6.5.

6.2 Use of the algorithm on the UDM/ARPF side p. 10

When generating a 5G HE AV comprising (RAND, AUTN, XRES*, KAUSF), the function f0 is first used to generate RAND, the details of which are outside the scope of the present document. Dependency on OPc and K is for simplicity omitted in the following.

The function f1 is used to generate MAC-A from RAND, and the current SQNHE and AMF, as available at the UDM/ARPF.
The function f5 is used to generate AK from RAND.
The AUTN is formed from AMF, SQN, AK and MAC-A (TS 33.102, TS 33.501), namely as AUTN = (SQNHE ⊕AK)|| AMF || MAC-A.
The function f2 is used to generate XRES from RAND.
The functions f3 and f4 are used to generate CK and IK, respectively, from RAND.
XRES* is generated from XRES, CK and IK, as described in Annex A of TS 33.501.
KAUSF is generated from (SQNHE EB AK), CK and IK, as described in Annex A of TS 33.501.

6.3 Use of the algorithm on the USIM and ME p. 11

Dependency on OPc and K is for simplicity omitted in the following. Upon receipt of RAND and AUTN = (SQNHE ⊕ AK) || AMF || MAC-A, the USIM (or eSIM) performs the following:

The function f5 is used to generate AK from RAND.
AK is used to extract the SQNHE-value from AUTN.
The SQNHE is compared with the local SQNMS, and if a mismatch is detected, the resynchronisation procedure of clause 6.4 takes place (TS 33.102, TS 33.501).
AMF is extracted from AUTN and the function f1 is used to generate a local XMAC-A value from RAND, SQNHE and AMF.
The locally generated XMAC-A is compared with the MAC-A value available as part of AUTN, and if a mismatch occurs, an authentication failure procedure takes place (TS 33.102, TS 33.501).
The USIM applies f2, f3, and f4 to RAND in order to generate RES, CK and IK, respectively, in analogy to steps 4 and 5 of clause 6.2. The USIM makes these values available to the ME.
The ME applies processing analogous to steps 6 and 7 of clause 6.2 in order to generate RES* and KAUSF from CK, IK, and the (SQNHE ⊕ AK) part of AUTN.

6.4 Use of the algorithm for resynchronization in the USIM p. 11

The resynchronisation token AUTS, carrying the protected value of SQNMS, is generated as follows (dependency on OPc and K is omitted for simplicity).

The function f1* is used to generate MAC-S from RAND, the current SQNMS and an all-zero AMF.
The function f5* is used to generate AK* from RAND.
The re-synch token AUTS is formed from SQNMS, AK* and MAC-S (TS 33.102, TS 33.501), namely as AUTS = (SQNMS ⊕ AK*) || MAC-S.

If the optional resynchronisation protection mechanism provided by f5** is used, then step 2 above shall be replaced by computing an AK* value by applying f5** to RAND and MAC-S.

6.5 Use of the algorithm for resynchronization in the UDM/ARPF p. 12

The resynchronisation token AUTS is used in the UDM/ARPF as follows (dependency on OPc and K is again omitted for simplicity).

The function f5* is used to generate AK* from RAND.
The quantity (SQNMS ⊕ AK*) is extracted from AUTS and XORed with AK*, giving (SQNMS ⊕ AK*) ⊕ AK* = SQNMS.
The function f1* is used to generate XMAC-S from RAND, the extracted SQNMS and an all-zero AMF.
MAC-S is extracted form AUTS and compared with the expected value XMAC-S.

If the optional resynchronisation protection mechanism provided by f5** is used, then step 1 above shall be replaced by computing an AK* value by applying f5** to RAND and the MAC-S available as part of AUTS.

6.6 Implementation aspects p. 12

All the f-functions have been designed so that they can be implemented on typical current IC cards and produce all output parameters in less than 500msec execution time.

6.7 Generic requirements on the authentication and key generation functions p. 12

Clause 4 in TS 33.105 provides generic requirements for all 3GPP cryptographic functions and algorithms. No corresponding document exists for the 5G setting, but parts assumed relevant for 5G are summarised below (in italics). Additional requirements and clarifications which were deemed necessary for the MILENAGE-256 context are also stated (in normal typeface).

Resilience

The functions should be designed with a view to their continued use for a period of at least 20 years. This includes resistance against possible advances in quantum computing. Successful attacks with a workload significantly less than exhaustive key search through the effective key space should be impossible. Attacks distinguishing outputs from random bit-strings of the same length should require effort meeting expectations for the target 256-bit security level.

The designers of above functions should design algorithms to a strength that reflects the above qualitative requirements.

World-wide availability and use

Legal restrictions on the use or export of equipment containing cryptographic functions may prevent the use of such equipment in certain countries.

It is the intention of the MILENAGE-256 design that UE and USIMs which embody these algorithms are unencumbered by restrictions on export or use, in order to allow the free circulation of 5G terminals. Network equipment, including UDM/ARPF, could be expected to come under more stringent restrictions.

6.8 Subsequent requirements on the authentication and key generation functions p. 13

MILENAGE-256 design employs Rijndael-256-256 ([8], [14]) as the kernel.

Part of the motivation for increasing the key length in MILENAGE-256 is to resist potential attacks involving quantum computers. Accordingly, it is assumed that, in addition to brute force key searches by a quantum computer, other attacks, judged feasible in the quantum computing model, were also to be considered. This matter is discussed in more detail in Document 4 (TR 35.937).

7 Algorithm design p. 13

Based on the requirements and fixed starting points, the following essential design criteria were established.

7.1 Design and evaluation criteria p. 13

Without knowledge of secret keys, the functions f1, f1*, f2, f3, f4, f5, f5* and f5** should be practically indistinguishable from independent random functions of their inputs RAND, SQN, and AMF.
It should be practically impossible to determine any part of the secret key K, or the operator variant algorithm configuration field, OP, by manipulation of the inputs and examination of the outputs to the algorithm.
Events tending to violate criteria 1 and 2 should be regarded as insignificant if they occur with probability approximately 2-256 (or require approximately 2256 operations) or less.
Events tending to violate criteria 1 and 2 should be examined if they occur with probability approximately 2-128 (or require approximately 2128 operations) to ensure they do not have serious consequences. Serious consequences would include recovery of a secret key or ability to emulate the algorithm on a large number of future inputs.
The design should build upon well-known structures and avoid unnecessary complexity. This will simplify analysis and avoid the need for a formal external evaluation.
The security analysis should, if possible, be further supported by a formal security proof covering the entire design or critical properties thereof.
Simple (hard-to-get-wrong) guidelines for how to securely perform operator customisation of the algorithms should be possible to state.
The algorithm set should be able to accept input parameters of different sizes and also produce output parameters of different sizes, and this flexibility should not introduce weaknesses, beyond those inherent to the selected parameter sizes.

Regarding (8), it is assumed (and also recommended) that, as a general principle, a specific implementation of MILENAGE-256 only supports a given set of parameter sizes among the possible choices. Exceptions from this principle could be motivated for certain parameters, e.g. the size of the subscriber key K and/or the size of RAND as part of a migration strategy towards increased security levels.

EXAMPLE:

An implementation could initially be deployed with 128-bit K and then later upgraded to 256-bit K.

7.2 Chosen design for the framework p. 14

The following diagram shows the MILENAGE-256 framework for the functions f1, f1*, f2, f3, f4, f5, f5* and f5** using the kernel function denoted PRFK.

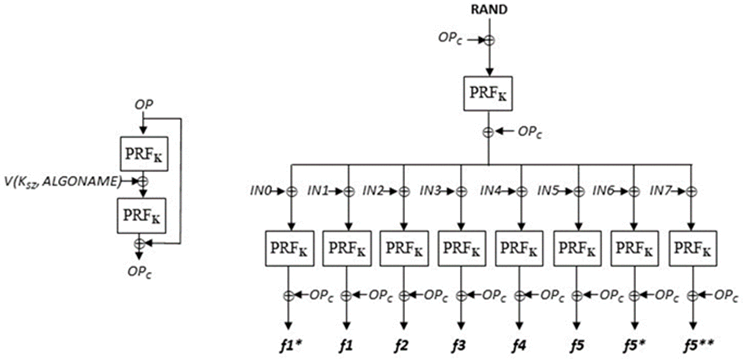
Copy of original 3GPP image for 3GPP TS 35.234, Fig. 7.2-1: MILENAGE-256 framework. Use of the functions f5* and f5** are mutually exclusive, i.e. precisely one of them is configured for use within an AKA protocol.

Figure 7.2-1: MILENAGE-256 framework. Use of the functions f5* and f5** are mutually exclusive, i.e. precisely one of them is configured for use within an AKA protocol.
(⇒ copy of original 3GPP image)

The value OPc is derived from the subscriber key K and the operator dependent value OP by

OPc ∶ 𝑂𝑃 ⊕ 𝑃𝑅𝐹(𝑃𝑅𝐹(OP ⊕ 𝑉(𝐾SZ,, 𝐴𝐿𝐺𝑂𝑁𝐴𝑀𝐸))

Here, the function V formats the size of the subscriber key KSZ and an encoding of the algorithm name into a 256-bit input to the PRF (TS 35.235).

It is recommended (TS 35.205) that OPc is calculated outside the USIM cards and then stored in each card as an individual value. This provides better protection for OP, relative to the alternative choice of storing OP in every card.

Each of the values IN0, IN1, … , IN7 appearing in Figure 7.2-1 comprises

an encoding of the function instance (i.e. which of the eight functions f1 to f5** is being computed).
encodings of the parameter sizes for any variable-size parameter that appears as input or output for the respective f-function.
for certain f-functions, additional input parameter(s), and
operator selectable customisation constants c0 , . . , c7 whose purpose is similar to those employed in MILENAGE (TS 35.205).

EXAMPLE:

Regarding (c) above, the function f1, as an example, takes SQN and AMF as additional inputs.

The encodings of IN0, IN1, … , IN7, as well as the inclusion of V() in the OP-derivation, serve to satisfy a cryptographic instance separation requirement: it would be highly unlikely that algorithm instances used in different contexts, or instances using/producing parameters of different sizes, result in the same (or otherwise correlated) outputs.

7.3 Analysis of the role of OP and OPC p. 15

The 256-bit value OP is the Operator Variant Algorithm Configuration Field, which was included to enable different operators to personalise the functionality of the algorithms. Each operator may freely select a value for OP.

The algorithm set is designed to be secure whether or not OP is publicly known; however, operators could benefit from keeping their value of OP secret, as an unknown OP value provides an additional hurdle for attackers.

It should be difficult for anyone who has discovered even a large number of (OPc, K) pairs to deduce OP. Consequently the OPc associated with any other value of K will be unknown, potentially making it (slightly) harder to mount some kinds of cryptanalytic and forgery attacks.

An operator is more likely to successfully keep OP secret if the value is not stored on the USIM; otherwise it would only require a single USIM to be reverse engineered for OP to be discovered and published. Hence, it is recommended that OPc is calculated off the USIM.

7.4 Choice of kernel / PRF p. 15

The MILENAGE-256 algorithms employ a kernel, denoted as PRFK. The algorithm set was designed to permit plug-in replacements for this kernel. This replaceability allows operators to freely employ variant kernels, without adversely impacting the security of the algorithm set, provided the replacement kernel is a suitable keyed function employing a 256-bit key. Candidate replacement kernels should satisfy certain general requirements (TS 35.235).

The qualitative security requirements on PRFK require that it is infeasible (or strongly believed to be infeasible) to distinguish the outputs of PRFK from the outputs of a randomly chosen function. The quantitative security requirements on PRFK require that the probability of distinguishing the output remains "small", even after observing on the order of ˜ 2¹²⁸ (input, output) pairs for chosen input-values. This latter constraint is the strongest requirement that can be satisfied if the kernel function is a 1-1 (permutation) mapping, such as a block cipher, in which case the PRF is actually a pseudo-random permutation (PRP). If the kernel function is not a permutation, stronger quantitative bounds are sometimes possible, allowing observation of a (much) larger number of (input, output) pairs.

MILENAGE-256 employs kernel, namely the block cipher Rijndael-256-256, which has 256-bit inputs/outputs and uses a 256-bit key ([8], [14]). Rijndael-256-256 was chosen owing to the extensive body of cryptanalysis and research already undertaken on the Rijndael family of block ciphers. Moreover, Rijndael block ciphers can be efficiently implemented in software or hardware and are generally held as being available IPR-free. The Rijndael-128-{128,192,256} algorithms were also selected as the AES (TS 33.501) and have been well studied in this context. MILENAGE-256 implements each PRFK instance as shown in Figure 7.2-1 by a straight-forward, single call of Rijndael-256-256.

7.5 Design methodology p. 15

The design process is summarised below.

The design of MILENAGE-256 was conducted quite quickly and problem-free since it could be based on a drop-in replacement, using Rijndael-256-256 instead of AES. In this phase it was also decided to simplify the operator customisation options, removing the input rotations and streamline the handling of the input offsets (the customisation constants c0 , . . , c7).

A review on the security status of the Rijndael was made without any discouraging findings.

Test vectors were also produced as the design choices were made and the design could be finalised.

7.6 Specification of the Test Data p. 15

The algorithm specification and associated test data are documented in the MILENAGE-256 specification (TS 35.236), where example program listings of the algorithm set in the C/C++ programming language also appear.

The Implementors' Test Data and Design Conformance Data document (TS 35.236) provides design conformance test data to help verify implementations of the algorithms. This document identifies intermediate points in the algorithms and provides input, internal and output parameters at these points, for use as test data. Different sets of test data listings are also provided.

8 Algorithm evaluation p. 16

8.1 Evaluation criteria p. 16

The algorithm requirements as summarised in clause 6 and design criteria as listed in clause 7.1 lead to evaluation criteria for the mathematical evaluation and statistical evaluations. Due to the fact that the Rijndael block cipher has undergone an extensive analysis, the Task Force performed no real cryptanalysis of Rijndael, but rather focused on the strength of the constructions for deriving the f1 to f5** modes from a strong block cipher. However, as mentioned, a survey of known attacks against AES/Rijndael was performed, including a verification of the cryptologic status of the 256-bit block version of Rijndael ([8], [14]).

8.2 Mathematical evaluation of the modes p. 16

The mathematical evaluation focused on verifying the strength of the f1-f5, f1*, f5*, and f5** constructions provided by MILENAGE-256, under the assumption that the underlying kernel is a strong block cipher. To be precise, more than one notion of "strong" is needed, see TR 35.937 for details.

The main criteria investigated were (TR 35.937):

The strength of each algorithm, considered individually (resilience of key and subsequent outputs).
The independence between algorithms (one algorithm's strength is not harmed by knowledge of input/outputs for other algorithms).

For MILENAGE-256, the "headroom" for possible insecurity depends only on how far from ideal Rijndael-256-256 is, when considered as a PRP. Roughly speaking, the security (in terms of indistinguishability from a random function) for MILENAGE-256 is provable up to about ˜ 2¹²⁸ queries by an attacker.

As noted, attacks involving possible future, cryptographically relevant quantum computers are briefly investigated in Document 4 of the specification (TR 35.937).

8.3 Statistical evaluation p. 16

Statistical tests on MILENAGE-256 were considered to only yield results about the underlying kernel function. No statistical tests were performed on the kernel either, given that AES and Rijndael can be considered to be sufficiently tested and secure through the AES process and later analysis.

8.4 Side channel attacks evaluation p. 16

The design process concluded that it was not feasible to design a general algorithm framework that, by itself, would not be vulnerable to side channel attacks. AES/Rijndael, as with most other block ciphers, is potentially vulnerable to simple and differential power analysis (SPA and DPA) aiming to recover the secret key. It was also concluded that the use of operator constants, OPc, in the USIM cards can only play a limited role in protecting against these kinds of attacks. In general, any implementation without dedicated protection against power or electromagnetic emanations (EM)-based side-channel attacks could be vulnerable to such attacks. Deployment scenarios in which an attacker is assumed to have the power to mount such attacks require protected implementations, e.g. by masking. Also timing attacks (TA) could require implementation specific countermeasures. Rijndael, as the AES, has been shown to readily lend itself to protection measures against side channel attacks.

8.5 Complexity evaluation p. 16

Implementations of Rijndael with 256-bit block- and key size could be two times slower than AES with 128-bit block size and the same key size.

Optimised implementations could also save computational costs. For example, the need to compute f1* and f5* implies that computation of f2, f3, and f4 is not needed, etc.

8.6 Evaluation report p. 17

The evaluation report (TR 35.937) summarises all results of the complete design and evaluation process, and provides the main conclusions of the evaluation work.