Content for TS 23.032 Word version: 18.3.0
5 Shapes
5.1 Ellipsoid Point
5.2 Ellipsoid point with uncertainty circle
5.3 Ellipsoid point with uncertainty ellipse
5.3a High Accuracy Ellipsoid point with uncertainty ellipse
5.3b High Accuracy Ellipsoid point with scalable uncertainty ellipse
5.4 Polygon
5.5 Ellipsoid Point with Altitude
5.6 Ellipsoid point with altitude and uncertainty ellipsoid
5.6a High Accuracy Ellipsoid point with altitude and uncertainty ellipsoid
5.6b High Accuracy Ellipsoid point with altitude and scalable uncertainty ellipsoid
5.7 Ellipsoid Arc
5.8 Local 2D point with uncertainty ellipse
5.9 Local 3D point with uncertainty ellipsoid
5.10 Range and Direction
5.11 Relative 2D Location with uncertainty ellipse
5.12 Relative 3D Location with uncertainty ellipsoid
...
...
5 Shapes p. 8
The intention is to incorporate a number of different shapes, that can be chosen according to need.
- Ellipsoid Point;
- Ellipsoid point with uncertainty circle;
- Ellipsoid point with uncertainty ellipse;
- Polygon;
- Ellipsoid point with altitude;
- Ellipsoid point with altitude and uncertainty ellipsoid;
- Ellipsoid Arc;
- High Accuracy Ellipsoid point with uncertainty ellipse;
- High Accuracy Ellipsoid point with scalable uncertainty ellipse;
- High Accuracy Ellipsoid point with altitude and uncertainty ellipsoid;
- High Accuracy Ellipsoid point with altitude and scalable uncertainty ellipsoid.
- Local 2D point with uncertainty ellipse (only in 5GS);
- Local 3D point with uncertainty ellipsoid (only in 5GS).
- Range and Direction (only in 5GS);
- Relative Location (only in 5GS).
5.1 Ellipsoid Point p. 9
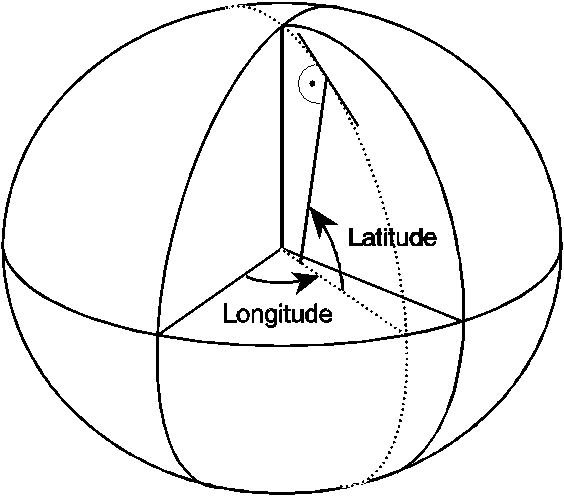
The description of an ellipsoid point is that of a point on the surface of the ellipsoid and consists of a latitude and a longitude. In practice, such a description can be used to refer to a point on Earth's surface, or close to Earth's surface, with the same longitude and latitude. No provision is made in this version of the standard to give the height of a point.
Figure 1 illustrates a point on the surface of the ellipsoid and its co-ordinates.
The latitude is the angle between the equatorial plane and the perpendicular to the plane tangent to the ellipsoid surface at the point. Positive latitudes correspond to the North hemisphere. The longitude is the angle between the half-plane determined by the Greenwich meridian and the half-plane defined by the point and the polar axis, measured Eastward.
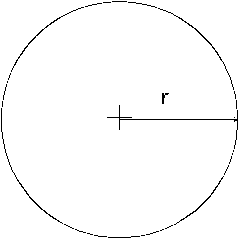
5.2 Ellipsoid point with uncertainty circle p. 9
The "ellipsoid point with uncertainty circle" is characterised by the co-ordinates of an ellipsoid point (the origin) and a distance r. It describes formally the set of points on the ellipsoid which are at a distance from the origin less than or equal to r, the distance being the geodesic distance over the ellipsoid, i.e. the minimum length of a path staying on the ellipsoid and joining the two points, as shown in Figure 2.
As for the ellipsoid point, this can be used to indicate points on the Earth surface, or near the Earth surface, of same latitude and longitude.
The typical use of this shape is to indicate a point when its position is known only with a limited accuracy.
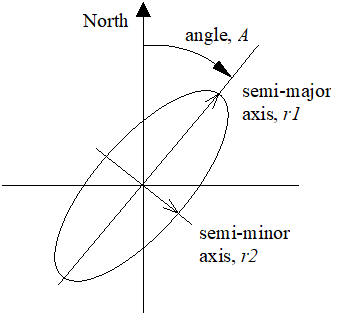
5.3 Ellipsoid point with uncertainty ellipse p. 10
The "ellipsoid point with uncertainty ellipse" is characterised by the co-ordinates of an ellipsoid point (the origin), distances r1 and r2 and an angle of orientation A. It describes formally the set of points on the ellipsoid which fall within or on the boundary of an ellipse with semi-major axis of length r1 oriented at angle A (0 to 180°) measured clockwise from north and semi-minor axis of length r2, the distances being the geodesic distance over the ellipsoid, i.e. the minimum length of a path staying on the ellipsoid and joining the two points, as shown in Figure 2a.
As for the ellipsoid point, this can be used to indicate points on the Earth's surface, or near the Earth's surface, of same latitude and longitude. The confidence level with which the position of a target entity is included within this set of points is also included with this shape.
The typical use of this shape is to indicate a point when its position is known only with a limited accuracy, but the geometrical contributions to uncertainty can be quantified.
5.3a High Accuracy Ellipsoid point with uncertainty ellipse p. 10
The "high accuracy ellipsoid point with uncertainty ellipse" is characterised by the co-ordinates of an ellipsoid point (the origin), distances r1 and r2 and an angle of orientation A, as described in clause 5.3. Compared to the "ellipsoid point with uncertainty ellipse", the "high accuracy ellipsoid point with uncertainty ellipse" provides finer resolution for the co-ordinates and distances r1 and r2.
5.3b High Accuracy Ellipsoid point with scalable uncertainty ellipse p. 10
The "high accuracy ellipsoid point with scalable uncertainty ellipse" is characterised by the co-ordinates of an ellipsoid point (the origin), distances r1 and r2 and an angle of orientation A, as described in clause 5.3. Compared to the "ellipsoid point with uncertainty ellipse", the "high accuracy ellipsoid point with scalable uncertainty ellipse" provides finer resolution for the co-ordinates and distances r1 and r2 and additionally provides possibility to choose uncertainty range compared to "high accuracy ellipsoid point with uncertainty ellipse".
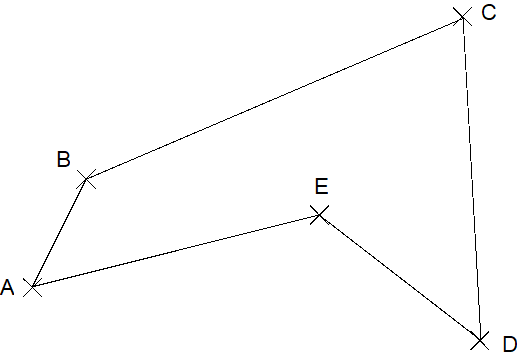
5.4 Polygon p. 11
A polygon is an arbitrary shape described by an ordered series of points (in the example pictured in the drawing, A to E). The minimum number of points allowed is 3 and the maximum number of points allowed is 15. The points shall be connected in the order that they are given. A connecting line is defined as the line over the ellipsoid joining the two points and of minimum distance (geodesic). The last point is connected to the first. The list of points shall respect a number of conditions:
- a connecting line shall not cross another connecting line;
- two successive points must not be diametrically opposed on the ellipsoid.
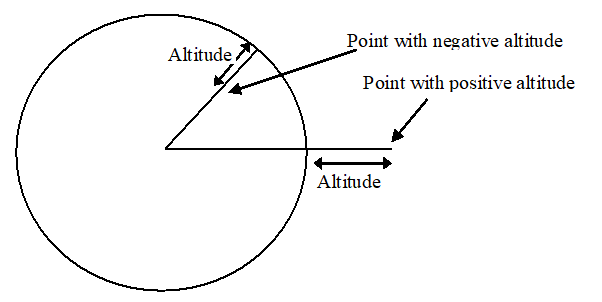
5.5 Ellipsoid Point with Altitude p. 11
The description of an ellipsoid point with altitude is that of a point at a specified distance above or below a point on the earth's surface. This is defined by an ellipsoid point with the given longitude and latitude and the altitude above or below the ellipsoid point. Figure 3a illustrates the altitude aspect of this description.
5.6 Ellipsoid point with altitude and uncertainty ellipsoid p. 12
The "ellipsoid point with altitude and uncertainty ellipsoid" is characterised by the co-ordinates of an ellipsoid point with altitude, distances r1 (the "semi-major uncertainty"), r2 (the "semi-minor uncertainty") and r3 (the "vertical uncertainty") and an angle of orientation A (the "angle of the major axis"). It describes formally the set of points which fall within or on the surface of a general (three dimensional) ellipsoid centred on an ellipsoid point with altitude whose real semi-major, semi-mean and semi-minor axis are some permutation of r1, r2, r3 with r1 ≥ r2. The r3 axis is aligned vertically, while the r1 axis, which is the semi-major axis of the ellipse in a horizontal plane that bisects the ellipsoid, is oriented at an angle A (0 to 180 degrees) measured clockwise from north, as illustrated in Figure 3b.
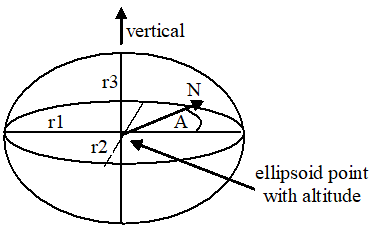
The typical use of this shape is to indicate a point when its horizontal position and altitude are known only with a limited accuracy, but the geometrical contributions to uncertainty can be quantified. The confidence level with which the position of a target entity is included within the shape is also included.
5.6a High Accuracy Ellipsoid point with altitude and uncertainty ellipsoid p. 12
The "high accuracy ellipsoid point with altitude and uncertainty ellipsoid" is characterised by the co-ordinates of an ellipsoid point with altitude, distances r1 (the "semi-major uncertainty"), r2 (the "semi-minor uncertainty") and r3 (the "vertical uncertainty") and an angle of orientation A (the "angle of the major axis"), as described in clause 5.6. Compared to the "ellipsoid point with altitude and uncertainty ellipsoid", the "high accuracy ellipsoid point with altitude and uncertainty ellipsoid" provides finer resolution for the co-ordinates and distances r1, r2 and r3.
5.6b High Accuracy Ellipsoid point with altitude and scalable uncertainty ellipsoid p. 13
The "high accuracy ellipsoid point with altitude and scalable uncertainty ellipsoid" is characterised by the co-ordinates of an ellipsoid point with altitude, distances r1 (the "semi-major uncertainty"), r2 (the "semi-minor uncertainty") and r3 (the "vertical uncertainty") and an angle of orientation A (the "angle of the major axis"), as described in clause 5.6. Compared to the "ellipsoid point with altitude and uncertainty ellipsoid", the "high accuracy ellipsoid point with altitude and scalable uncertainty ellipsoid" provides finer resolution for the co-ordinates and distances r1, r2 and r3 and additionally provides possibility to choose uncertainty range compared to "high accuracy ellipsoid point with altitude and uncertainty ellipse".
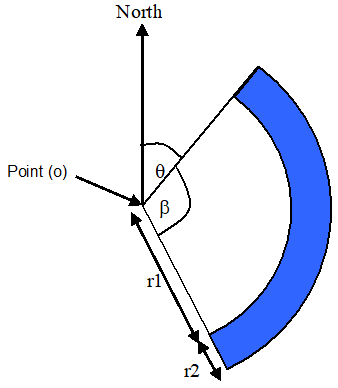
5.7 Ellipsoid Arc p. 13
An ellipsoid arc is a shape characterised by the co-ordinates of an ellipsoid point o (the origin), inner radius r1, uncertainty radius r2, both radii being geodesic distances over the surface of the ellipsoid, the offset angle (θ) between the first defining radius of the ellipsoid arc and North and the included angle (β) being the angle between the first and second defining radii. The offset angle is within the range of 0° to 359,999…° while the included angle is within the range from 0,000…1° to 360°. This is to be able to describe a full circle, 0° to 360°.
This shape-definition can also be used to describe a sector (inner radius equal to zero), a circle (included angle equal to 360°) and other circular shaped areas. The confidence level with which the position of a target entity is included within the shape is also included.
5.8 Local 2D point with uncertainty ellipse p. 13
The "local 2D point with uncertainty ellipse" is characterised by a point described in 2D local co-ordinates with origin in a known reference location, distances r1 and r2 and an angle of orientation A. The local Cartesian co-ordinates system and the reference location shall be identified with a unique identifier. It describes formally the set of points which fall within or on the boundary of an ellipse with semi-major axis of length r1 oriented at angle A (0 to 180°) measured clockwise from north and semi-minor axis of length r2. The confidence level with which the position of a target entity is included within this set of points is also included with this shape.
This shape is only applicable to 5GS.
The structure of local 2D point with uncertainty ellipse is defined in clause 6.1.6.2.38 in TS 29.572.
5.9 Local 3D point with uncertainty ellipsoid p. 14
The "local 3D point with uncertainty ellipsoid" is characterised by a point described in 3D local co-ordinates with origin in a known reference location, distances r1 (the "semi-major uncertainty"), r2 (the "semi-minor uncertainty") and r3 (the "vertical uncertainty") and an angle of orientation A (the "angle of the major axis"). The local Cartesian co-ordinates system and the reference location shall be identified with a unique identifier. It describes formally the set of points which fall within or on the surface of a general (three dimensional) ellipsoid centred on a 3D point whose real semi-major, semi-mean and semi-minor axis are some permutation of r1, r2, r3 with r1 ≥ r2. The r3 axis is aligned vertically, while the r1 axis, which is the semi-major axis of the ellipse in a horizontal plane, is oriented at an angle A (0 to 180 degrees) measured clockwise from north. The confidence level with which the position of a target entity is included within the shape is also included.
This shape is only applicable to 5GS.
The structure of local 3D point with uncertainty ellipsoid is defined in clause 6.1.6.2.39 in TS 29.572.
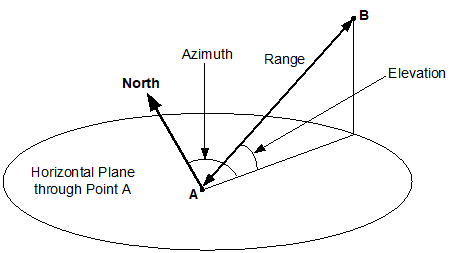
5.10 Range and Direction p. 14
The "range and direction" from a point A to a point B is characterised by three components comprising a range from point A to point B, an azimuth direction from point A to point B and an elevation direction from point A to point B as shown in Figure 3d. The range provides a straight-line distance from point A to point B. The azimuth provides a direction to point B from point A in a horizontal plane through point A and as measured clockwise from North. The elevation provides a direction to point B from point A in a vertical plane through the points A and B and as measured upwards or downwards from a horizontal plane through point A. The range, azimuth and elevation can be each independently included or excluded in a "range and direction" and each has an uncertainty and a confidence.
5.11 Relative 2D Location with uncertainty ellipse p. 14
The "relative 2D location with uncertainty ellipse" is characterised by a point described in 2D local co-ordinates with origin corresponding to another known point, distances r1 and r2 and an angle of orientation A. It describes formally a set of points which fall within or on the boundary of an ellipse cantered on a 2D point with semi-major axis of length r1 oriented at angle A (0 to 180°) measured clockwise from North and semi-minor axis of length r2. The confidence level with which the position of a target entity is included within this set of points is also included with this shape.
This shape is only applicable to 5GS.
5.12 Relative 3D Location with uncertainty ellipsoid p. 14
The "relative 3D location with uncertainty ellipsoid" is characterised by a point described in 3D local co-ordinates with origin corresponding to another known point, distances r1 (the "semi-major uncertainty"), r2 (the "semi-minor uncertainty") and r3 (the "vertical uncertainty") and an angle of orientation A (the "angle of the major axis"). It describes formally the set of points which fall within or on the surface of a general (three dimensional) ellipsoid centred on a 3D point whose semi-major, semi-minor and semi-mean axis are, respectively, r1, r2, r3 with r1 ... r2. The r3 axis is aligned vertically, while the r1 axis, which is the semi-major axis of the ellipse in a horizontal plane, is oriented at an angle A (0 to 180 degrees) measured clockwise from North. The confidence level with which the position of a target entity is included within the shape is also included.
This shape is only applicable to 5GS.